Pseudo-random Number Dice(유사난수 주사위)

오랜만에 대학 동기에게 연락이 왔습니다. 말년 휴가 중인 걸 알고 있었는지 학과 내 학술 소모임 카카오톡 단체 방에 초대해주겠다는 이야기였습니다. 늘 카카오톡은 휴대폰에 용량만 차지하던 장식이었는데 알림이 뜨기 시작한게 얼마 만인지 모르겠습니다. 그래도 시간은 가고 제대라는게 오긴 오고 있는가 봅니다.

슬슬 복학 준비도 해야겠다 싶어 옛 자료를 뒤져보는 중, 재미난걸 발견했습니다. 2017년 06월 08일, 날짜도 적혀 있습니다. 기초전자공학실험 수업에서 만들었던 작품에 대한 자료가 있네요. 아직도 기억이 나는 게, 그 수업 교수님께서 두 가지 옵션을 주셨습니다. 하나는 교수님께서 제시한 주제인 14 mod 카운터 구현, 또 다른 하나는 자유주제였습니다.

교수님 왈, 정해진 주제에 대한 프로젝트를 진행하는 경우 절대 A+를 줄 수 없다 하셨습니다. 그래서 어쩔 수 없이 자유 주제를 택했습니다. 점수는 잘 받는게 좋으니. 그런데 이제 막 2학년으로 올라간 학생이 전자공학 주제에 관해 뭘 알겠습니까. 이것 저것 찾아보고 괜찮겠다 싶었던게 이 pseudo-random number dice(유사난수 주사위)였습니다.

이것 저것 삽질하고, 처음 만져보는 칩 명령어도 제대로 찾지 못해 오랫동한 고생했던 경험은 잊을 수가 없습니다. 어차피 다시 학교로 돌아가야 하니 복습하는 겸 옛 자료를 다시 꺼내보겠습니다.

개요

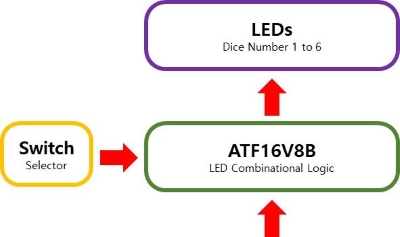
목적은 단순합니다. 7개의 LED를 이용하여 주사위를 던지는 결과 값을 출력하는 회로를 제작하는겁니다.

주사위는 수학적으로는 1/6의 확률로 부터 까지의 수를 얻습니다. 이를 7개의 LED를 주사위의 점 모양으로 배치해 결과를 출력합니다. 이때, 주사위의 결과는 무작위의 값에 의해 결정되므로 난수를 생성하는 회로가 필요할겁니다. 회로의 전체적인 개요는 다음과 같습니다.

난수 생성부는 D 플립플롭이 선형적으로 연결되어 있는 구조인 선형 되먹임 시프트 레지스터(Linear Feedback Shift Register, LFSR)를 이용합니다.
의사난수의 경우 LFSR으로 생성된 수열의 길이가 길면 길수록 난수에 가까워집니다. 따라서 Pseudo-random Dice에서 사용될 LFSR는 16-bit의 레지스터를 이용합니다. 16-bit으로 생성되는 의사난수는 이론적으로 의 65,535의 주기를 갖게 됩니다.
표시부 에서는 주사위는 부터 까지의 값을 표현하도록 합니다. 따라서 연속적으로 생성된 3-bit를 이용해 값을 출력합니다.

뭐, 7개의 LED는 다음과 같은 모양으로 배치하면 될 겁니다. 생성되는 수에 맞게 아래와 같이 출력하도록 설정합시다.

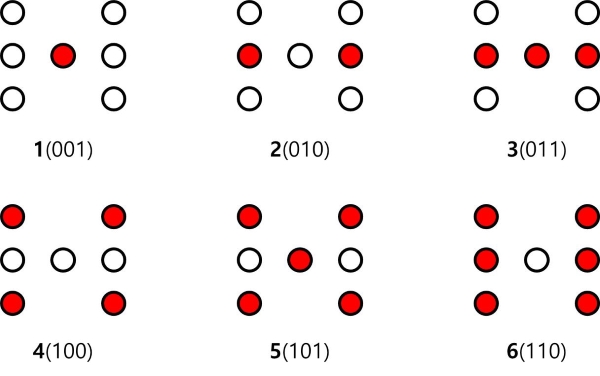
(1) 배경 이론

완벽한 난수를 회로로 구성하는 것은 굉장히 난해합니다. 따라서 유사난수 회로를 구현하는 것으로 합시다. 여기에 선형 되먹임 시프트 레지스터(Linear Feedback Shift Register, LFSR)가 사용되므로 간단히 원리를 알아봅시다.

이전에 참고했던 사이트(링크)가 지금 확인해 보니 죽어있습니다. 지금은 좋은 자료가 많이 있으니 다른 사이트의 자료를 참고하시면 될 듯 싶습니다.

선형 되먹임 시프트 레지스터(LFSR)는 시프트 레지스터의 일종으로, 레지스터에 입력되는 값이 이전 상태 값들의 선형 함수로 계산되는 구조를 가지고 있습니다. 의사난수 생성기(Pseudo-random Number Generator)는 LFSR로 구성되는데, 이때 사용되는 선형 함수(피드백)는 주로 배타적 논리합(XOR)입니다. LFSR의 초기 bit 값은 시드(seed)라고 부릅니다.

LFSR를 이용한 에서 생성되는 값의 수열은 그 이전 값에 의해 결정됩니다. 또한, 레지스터가 가질 수 있는 값의 수는 유한하므로 이 수열은 특정한 주기에 의해 반복됩니다. 하지만 선형 함수를 잘 선택한다면 주기가 길고 무작위적으로 보이는 수열을 생성할 수 있습니다.

LFSR은 크게 다음과 같은 두 가지 방식으로 적용하는데 Fibonacci Implementation과 Galois Implementation입니다. 두 개의 방식 모두 동일한 수열을 생성하나 초기 조건은 다를 수 있습니다. 이때 주어지는 초기 조건은 Fibonacci Implementation의 경우 Initial Fill 또는 Initial Vector라고 하며 Galois Implementation 의 경우 Seed라고 부릅니다.

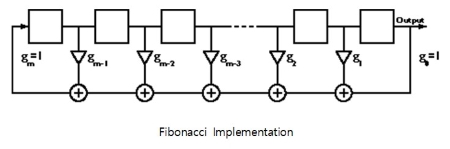
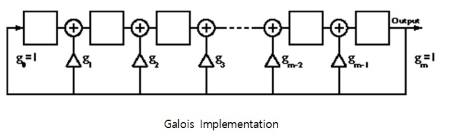
피드백에 영향을 주는 비트 위치를 탭(Tap)이라고 합니다. 탭의 목록을 탭 수열이라고 하는데, 예를 들어 탭이 16번째, 14번째, 13번째 및 11번째 비트라면 [16, 14, 13, 11]과 같이 표현합니다. 다항식으로도 표현이 가능한데 LFSR 다항식은 아래와 같습니다.

\[x^{16}+x^{14}+x^{13}+x^{11}+1\]

LFSR은 Linear Recursive Sequences(LRS)라는 수열을 생성하는데 이는 모든 연산이 선형적인 구조를 가지고 있기 때문입니다.

일반적으로 LFSR로 생성된 수열의 반복은 사용되는 D 플립플롭의 개수와 초기 값(seed)이라는 두 가지 요소에 의해 결정됩니다. LFSR을 구성하는 플립플롭의 수가 \(m\)개인 경우, 수열의 주기는 다음과 같습니다.

\[N=2^m-1\]

그러나 이 주기는 적절한 피드백(Feedback)이 일어난 경우에 최대의 값인 \(N\)을 가지게 됩니다. 어떤 하나의 LFRS가 \(N\)이라는 최대 주기를 가지게 되는 경우를 Maximal Length Sequence라고 하며 M-Sequence라고도 부릅니다. M-Sequence는 다음과 같은 특성을 갖습니다.

LFSR는 탭의 수가 짝수일 경우에만 최대입니다.
최대 LFSR에서 탭 값은 서로소입니다.
m-bit의 레지스터는 \(N=2^m-1\)의 주기를 갖습니다.
M-Sequence는 정확히 \(2^m-1\)개의 0과 1을 갖습니다.
최대 탭 수열이 발견되면 나머지는 자동으로 따릅니다. \(n\)비트 LFSR에서 탭 수열이 [\(n\), \(A\), \(B\), \(C\), \(0\)]이면 0은 \(x^0=1\)항과 일치하고, 일치한 ‘거울’ 수열은 [\(n\), \(n-C\), \(n-B\), \(n-A\), \(0\)]입니다.

(2) 난수 생성부

난수 생성부에서는 16-bit LFSR를 이용한 의사난수 생성기를 사용하겠습니다. Linear Shift Register로는 16V8을 이용합니다. 이때, 의사난수 생성기가 정상적으로 작동하기 위해서는 모든 bit가 0이 아닌 초기값(seed)를 주어야만 할 것입니다.

아래는 구성도의 일부입니다.

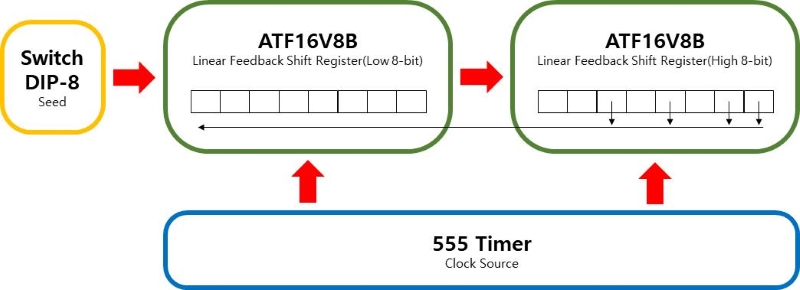
이렇게 합시다.

M-Sequence가 정상적으로 작동하기 위해서는 모든 bit가 0이 되는 경우를 배제해야 하므로 D 플립플롭과 스위치을 이용합니다. 이때 D 플립플롭은 16V8을 프로그래밍 하여 사용하도록 합니다.

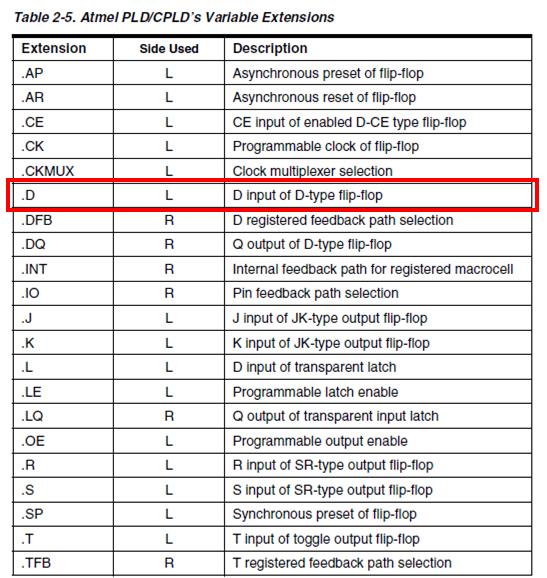
M-Sequence의 적용 방법은 위의 Galois Implementation을 이용합니다. 그래야 납땜할 선의 개수가 적어집니다.
의사난수 생성기가 정상적으로 작동하기 위해서는 모든 bit가 이 아닌 초기값(seed)를 주어야 한다고 했습니다. 따라서 인위적으로 매번 값을 다르게 넣을 수 있도록 DIP-8 스위치를 사용하여 최하위 4-bit에 0이 아닌 초기값을 입력하도록 설계합니다.
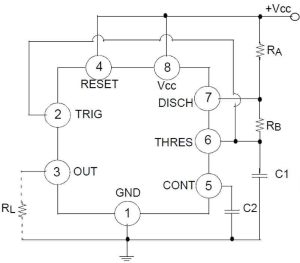
555 타이머는 비안정(Astable)모드로 동작합니다. 이를 위해 위 그림처럼 RA, RB, C1을 추가해야 하며 그래야 C1의 방전을 통해 낮아진 전압이 Trigger입력에 반영 될겁니다. 비안정 모드에서 Output은 일정한 주기로 반복됩니다.

비안정 모드에서 Output의 주파수는 다음과 같습니다.

타이머의 경우 속도를 조절할 수 있도록 하기 위해 \(R_A=100\)K, \(C_1=1\)uF, \(R_B\)는 가변저항을 사용합시다.
\

\[f=\frac{1.44}{(R_A+2R_B)C_1}\]

Maximum Length Sequence를 발생시키기 위해 XOR연산이 필요합니다. 이는 구성도에서 위쪽 부분의 16V8가 담당하도록 합니다.

M-Sequence를 발생시키는 데에는 모든 레지스터의 출력이 필요한 것이 아닙니다. 다음은 16-bit 일 때 M-Sequence를 발생시키는 탭 수열 표의 일부입니다.

16 stages, 4 taps: (26 sets)	16 stages, 6 taps: (184 sets)
[16, 15, 13, 4]	[16, 15, 14, 13, 12, 11]
[16, 15, 12, 10]	[16, 15, 14, 13, 11, 8]
[16, 15, 12, 1]	[16, 15, 14, 13, 11, 7]
[16, 15, 10, 4]	[16, 15, 14, 13, 10, 8]
[16, 15, 9, 6]	[16, 15, 14, 13, 10, 4]
[16, 15, 9, 4]	[16, 15, 14, 13, 9, 3]
[16, 15, 7, 2]	[16, 15, 14, 13, 6, 5]
[16, 15, 4, 2]	[16, 15, 14, 13, 6, 3]
[16, 14, 13, 11]	[16, 15, 14, 13, 6, 2]
…	…

위의 표에서 간단한 [16, 14, 13, 11]의 경우를 설정하고 XOR 연산을 WinCUPL을 이용하여 구현합시다.

(3) 표시부

표시부는 난수 생성부로부터 얻은 최상위 3-bit의 연속적인 결과를 입력받습니다. 이 때 7개의 LED를 주사위의 모양으로 출력하기 위해서 다음과 같은 과정이 필요합니다.

① 위의 모양으로 LED를 배치한 후 아래와 같이 구분하도록 합니다.

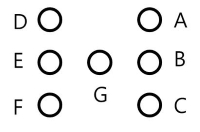
1부터 6까지의 범위이므로 총 3-bit가 필요하며 각 경우의 수마다 출력되어야 하는 LED의 위치가 달라집니다. 따라서 모양에 맞도록 아래와 같이 진리표를 작성하면 됩니다.

I2	I1	I0	A	B	C	D	E	F	G
0	0	0	x	x	x	x	x	x	x
	0	1	0	0	0	0	0	0	0
	1	0	0	1	0	0	1	0	0
	1	1	0	1	0	0	1	0	1
1	0	0	1	0	1	1	0	1	0
	0	1	1	0	1	1	0	1	1
	1	0	1	1	1	1	1	1	0
	1	1	x	x	x	x	x	x	x

② 위의 진리표의 경우 표현할 수 없는 수인 과 에서는 정의하지 않았습니다. 그러나 위 진리표를 통해 K-map을 그릴 경우 이상한 주사위 모양이 나올 수 있어 모두 0으로 설정하겠습니다.

I2	I1	I0	A	B	C	D	E	F	G
0	0	0	0	0	0	0	0	0	0
	0	1	0	0	0	0	0	0	0
	1	0	0	1	0	0	1	0	0
	1	1	0	1	0	0	1	0	1
1	0	0	1	0	1	1	0	1	0
	0	1	1	0	1	1	0	1	1
	1	0	1	1	1	1	1	1	0
	1	1	0	0	0	0	0	0	0

이를 K-map을 그려 출력을 간단히 하면,

\[A = B = C = D = F = I2 \cdot ( I1 \cdot I0 )'\]

\[B = E = = I1 \cdot ( I2 \cdot I0 )'\]

\[G = I0 \cdot ( I2 \cdot I1 )'\]

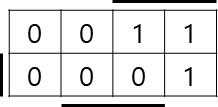
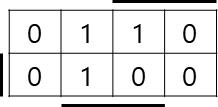
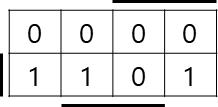
를 얻습니다. 위의 연산은 16V8를 이용해 구현하겠습니다.

구성도

전체적인 구성을 정리하면 다음과 같습니다.

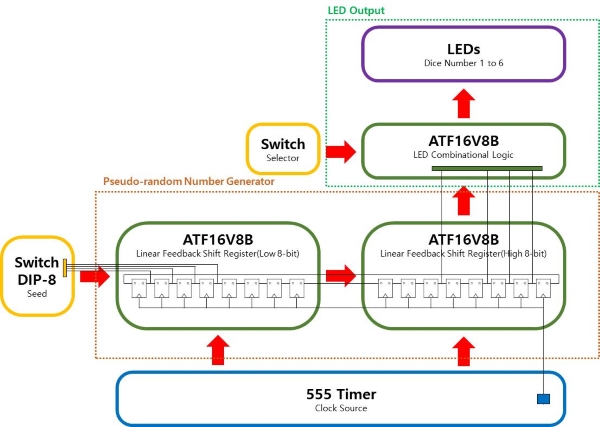
모의실험용 회로도 및 모의실험 결과

(1) 클럭원(555 Timer)

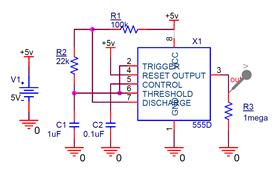
위와 같이 회로를 구성합니다. R2의 22KOhm는 제작 시 가변저항으로 대체할 겁니다. 모의실험 결과는 아래와 같습니다.

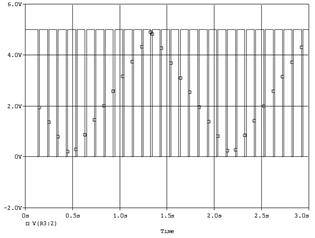
클럭이 정상적으로 출력되는 것을 확인할 수 있습니다.

(2) 난수 생성부 및 표시부

난수 생성부와 표시부의 경우 대부분 ATF16V8B가 이용되므로 모의실험은 WinSim을 이용하여 진행하겠습니다.

WinCUPL 코드 및 WinSim 모의실험

(1) Linear Shift Register(Low 8-bit)

① [16, 14, 13, 11]의 탭 수열을 적용하기 때문에 하위 8-bit Shift Register을 담당하는 16V8은 단순한 Shift Register의 역할을 합니다.

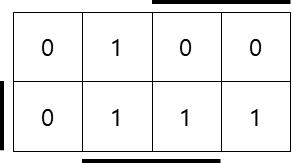
한편, 최하위 4-bit의 값을 입력하기 위해 Load의 입력을 받습니다. 이 때, 스위치를 단순하게 16V8에 연결하는 경우 클럭으로 인해 동일한 값만 Shift됩니다. 따라서 Load‘의 값이 1이 인가된 경우에만 DIP 스위치로 입력한 초기값이 들어가도록 구현합니다. 즉, 다음과 같이 진리표를 그리고, Boolean식을 K-map으로 간략화합니다.

Load	Seed	Reg	Reg+
0	0	0	0
	0	1	0
	1	0	1
	1	1	1
1	0	0	0
	0	1	1
	1	0	0
	1	1	1

\[Reg(N+1)_D = Load' \cdot Seed(N+1)+RegN \cdot Load\]

이를 코드로 구현하면 아래와 같습니다.

Name        LFSR_LOW_BIT ;
PartNo      00 ;
Date        2017-05-17 ;
Revision    01 ;
Designer     ;  
Company      ;
Assembly    None ;
Location     ;
Device      G16V8A ;

/* INPUTS */
PIN 1 = Clk ;
PIN 2 = Feedback ;
PIN 3 = Load ;
PIN [4..7] = [Seed0..3] ;

/* OUTPUTS */
PIN [12..19] = [Reg0..7] ;

/* OPERATION */
Reg0.D = (Feedback & Load) # (Seed0 & !Load) ;
Reg1.D = (Reg0 & Load) # (Seed1 & !Load) ;
Reg2.D = (Reg1 & Load) # (Seed2 & !Load) ;
Reg3.D = (Reg2 & Load) # (Seed3 & !Load) ;
Reg4.D = Reg3 ;
Reg5.D = Reg4 ;
Reg6.D = Reg5 ;
Reg7.D = Reg6 ;

② 다음은 WinSim 모의실험 결과입니다.

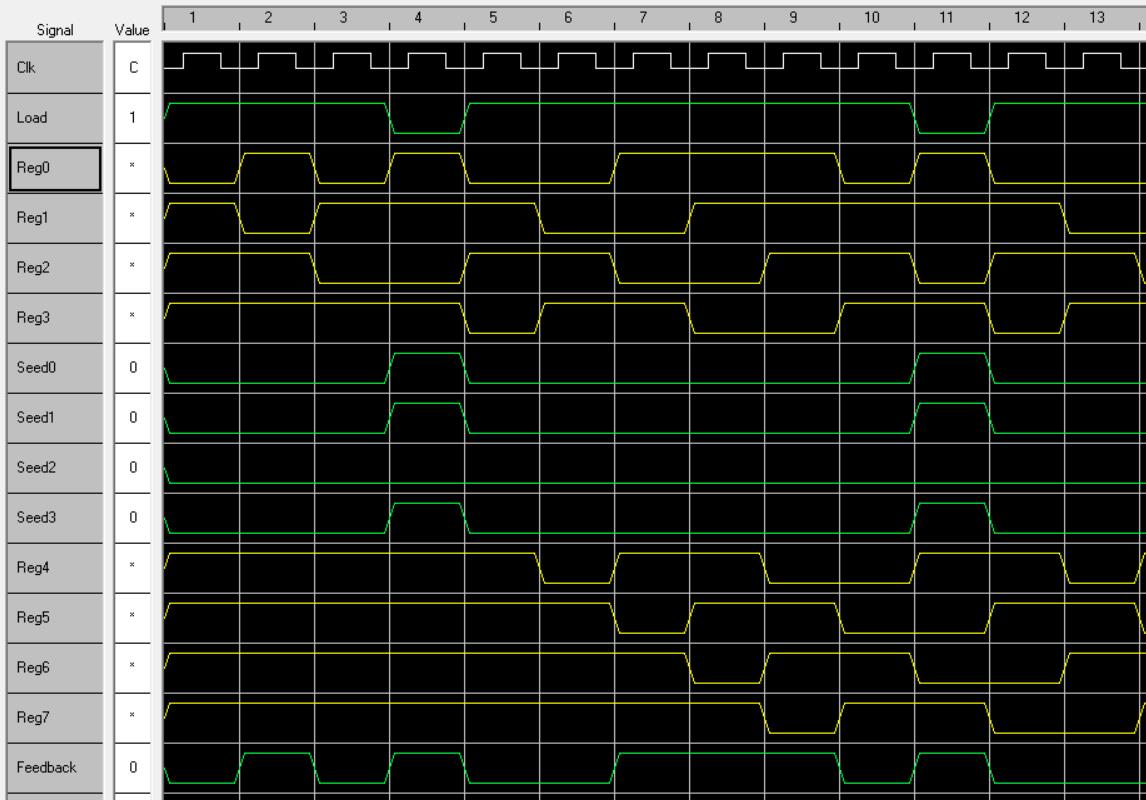
Load’가 1이 인가될 때 Seed0~Seed3의 값이 정상적으로 입력되고 클럭에 의해 다음 레지스터로 Shift 되는 것을 확인할 수 있습니다.

(2) Linear Shift Register(High 8-bit)

① M-Sequence를 발생시키는 탭 수열 중 [16, 14, 13, 11]를 선택하겠습니다. [16, 15, 12, 1]과 같은 수열을 선택하는 경우, 각각 구현할 탭이 두 개의 16V8로 분리되어 까다롭습니다. 따라서 상위 8-bit의 Shift Register를 담당하는 하나의 16V8로 XOR연산을 구현하기 위해 의 수열을 선택하도록 합시다.

또한, Fibonacci Implementation을 적용할 경우 최상위 bit와 각 탭의 bit을 연산하여 Feedback 시키는데, 이 때 외부에서 XOR연산을 담당하는 로직이 필요하므로 부품의 개수가 증가합니다. 따라서, 16V8 내에서 Shift Register의 역할과 동시에 XOR연산이 가능한 Galois Implementation을 적용하여 CUPL코드로 구현하겠습니다. 이는 아래와 같습니다.

Name        LFSR_HIGH_BIT ;
PartNo      00 ;
Date        2017-05-17 ;
Revision    01 ;
Designer     ;  
Company      ;
Assembly    None ;
Location     ;
Device      G16V8A ;

/* INPUTS */
PIN 1 = Clk ;
PIN 2 = Carry ;

/* OUTPUTS */
PIN [12..19] = [Reg8..15] ;

/* OPERATION */
Reg8.D = Carry ;
Reg9.D = Reg8 ;
Reg10.D = (Reg9 $ Reg15) ;
Reg11.D = Reg10 ;
Reg12.D = (Reg11 $ Reg15) ;
Reg13.D = (Reg12 $ Reg15) ;
Reg14.D = Reg13 ;
Reg15.D = (Reg14 $ Reg15) ;

② WinSim 모의실험 결과는 아래와 같습니다.

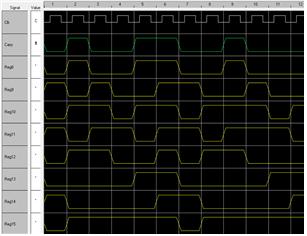
Reg10, Reg12, Reg13의 경우 이전 출력과 XOR되어 정상적으로 출력되는 것을 확인할 수 있습니다. 그 외의 경우 Shift되어 출력되고 있습니다.

(3) Combinational Logic for LEDs

① K-map으로 얻은 표시부의 출력 bit는 아래와 같은 부울 식을 따릅니다.

\[A = B = C = D = F = I2 \cdot ( I1 \cdot I0 )'\] \[B = E = I1 \cdot ( I2 \cdot I0 )'\] \[G = I0 \cdot ( I2 \cdot I1 )'\]

한편, 스위치를 적용하여 신호가 인가된 경우 클럭에 의해 bit가 쉬프트 되고, 신호가 인가되지 않은 경우 최근의 출력을 유지하도록 합니다. 따라서 Load‘의 입력을 추가하고 아래와 같이 진리표를 그립니다.

\[LED_n .D = Load' \cdot I2 \cdot (I1 \cdot I0)' + Load \cdot LED_n \ where, n=A, C, D, F\] \[LED_n .D = Load' \cdot I1 (I2 \cdot I0)' + Load \cdot LED_n \ where, n=B, E\] \[LED_G .D = Load' \cdot I0 (I2 \cdot I1)' + Load \cdot LED_G\]

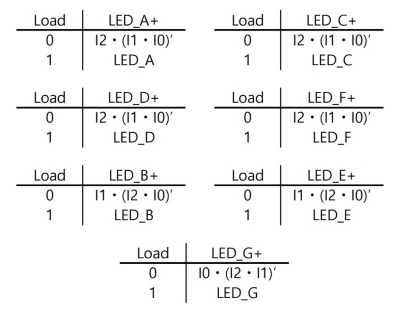
이에 대한 CUPL 코드는 다음과 같습니다.

Name        LFSR_LOGIC ;
PartNo      00 ;
Date        2017-05-17 ;
Revision    01 ;
Designer     ;  
Company      ;
Assembly    None ;
Location     ;
Device      G16V8A ;

/* INPUTS */
PIN 1 = Clk ;
PIN 2 = Load ;
PIN[3..5] = [I0..2] ;

/* OUTPUTS */
PIN 12 = LED_A ;
PIN 13 = LED_B ;
PIN 14 = LED_C ;
PIN 15 = LED_D ;
PIN 16 = LED_E ;
PIN 17 = LED_F ;
PIN 18 = LED_G ;


/* OPERATION */
LED_A.D = !Load & I2 & !(I1 & I0) # Load & LED_A ;
LED_C.D = !Load & I2 & !(I1 & I0) # Load & LED_C ;
LED_D.D = !Load & I2 & !(I1 & I0) # Load & LED_D ;
LED_F.D = !Load & I2 & !(I1 & I0) # Load & LED_F ;

LED_B.D = !Load & I1 & !(I2 & I0) # Load & LED_B ;
LED_E.D = !Load & I1 & !(I2 & I0) # Load & LED_E ;

LED_G.D = !Load & I0 & !(I2 )& I1 # Load & LED_G ;

② WinSim 모의실험 결과는 다음과 같습니다.

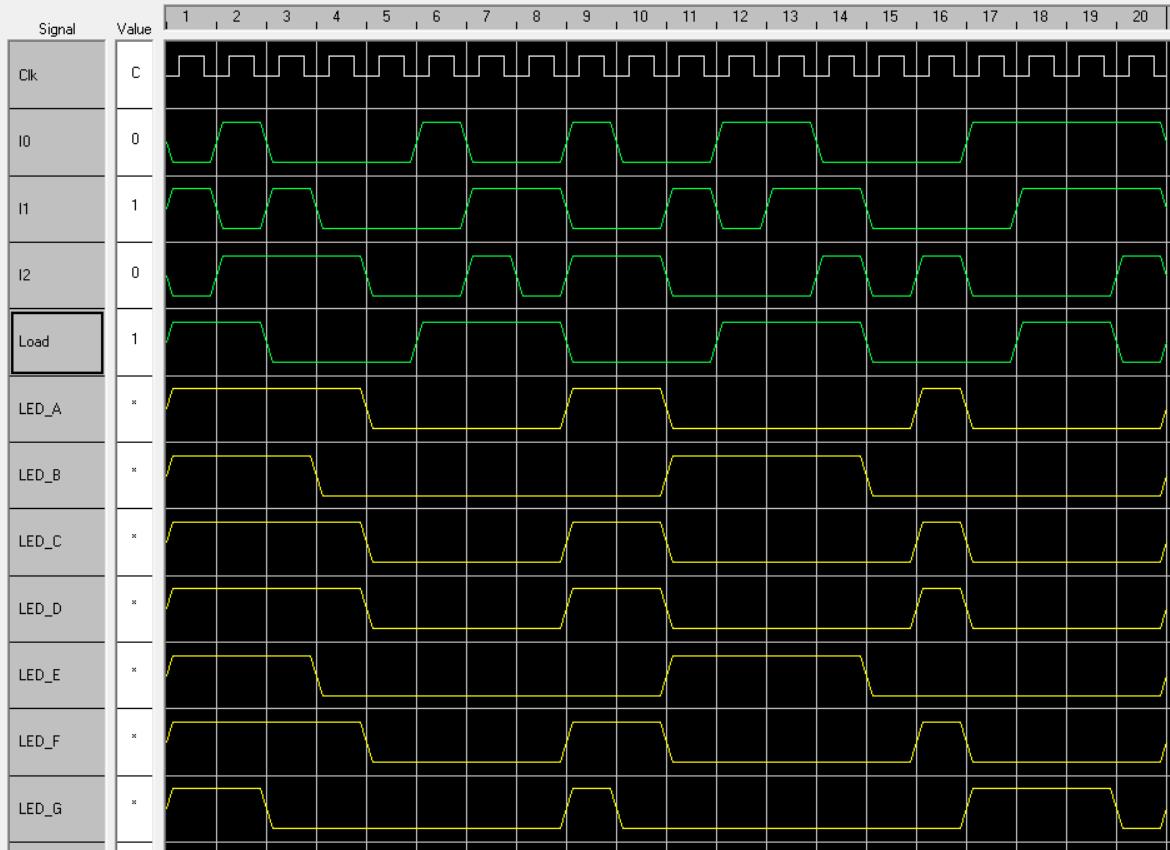
Load’가 1이 인가될 때 입력에 대한 각 LED로 신호가 정상적으로 입력되고 클럭에 의해 다음 계산 계산으로 진행되는 것을 확인할 수 있습니다. Load‘가 0이 인가될 때 직전의 LED값을 유지하는 것을 확인할 수 있습니다.

제작용 회로도

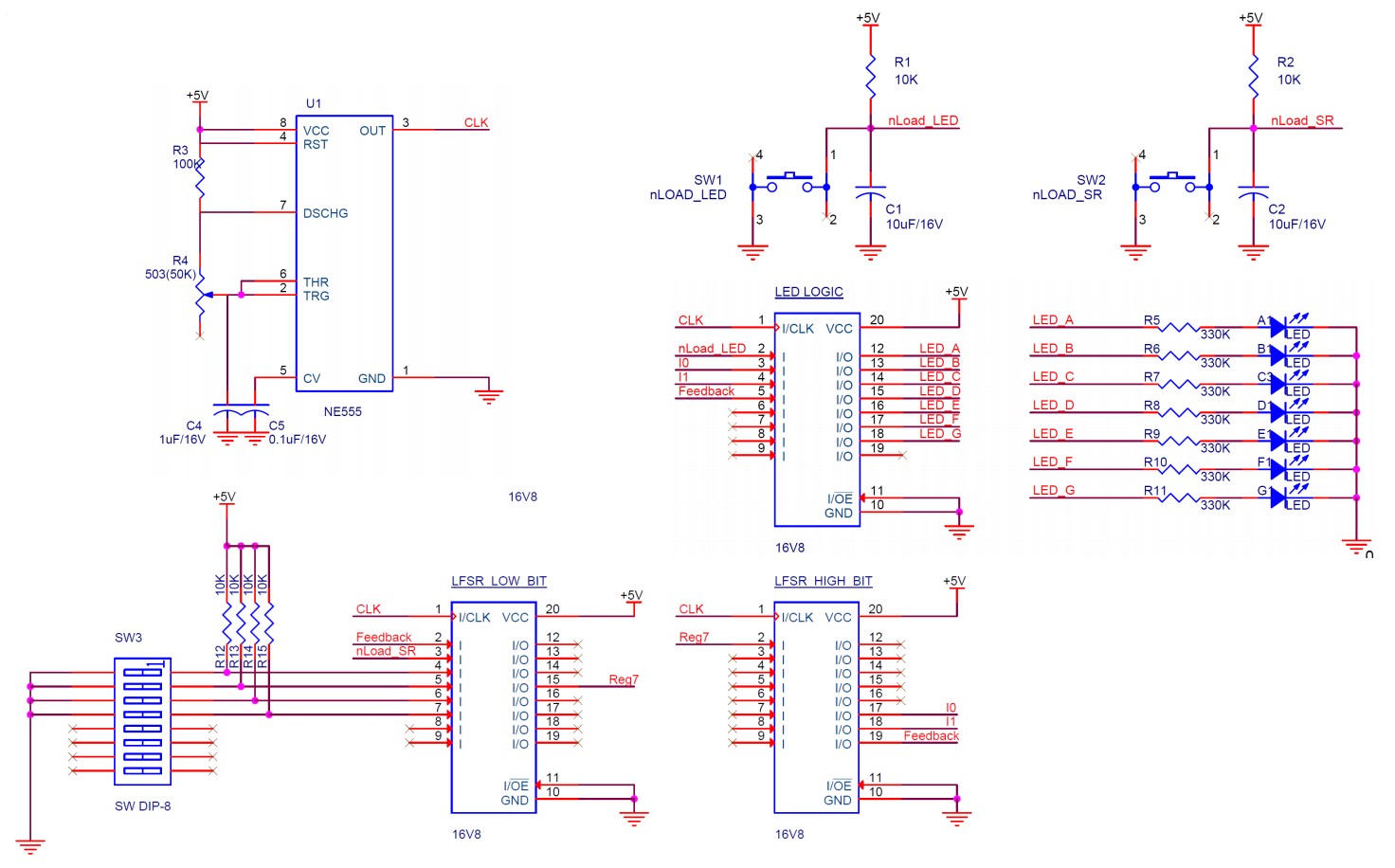
BOM

Revised: Thursday, May 18, 2017 Revision:

Bill Of Materials May 14, 2017 22:42:10 Page1

Item	Quantity	Reference	Part
1	7	G1,F1,E1,D1,B1,A1,C3	LED
2	2	C1,C2	10uF/16V
3	1	C4	1uF/16V
4	1	C5	0.1uF/16V
5	3	LFSR_LOW_BIT, 16V8 LFSR_HIGH_BIT,LED LOGIC
6	6	R1,R2,R12,R13,R14,R15	10K
7	1	R3	100K
8	1	R4	503(50K)
9	7	R5,R6,R7,R8,R9,R10,R11	330K
10	1	SW1	nLOAD_LED
11	1	SW2	nLOAD_SR
12	1	SW3	SW DIP-8
13	1	U1	NE555
14	3	SPLD용 DIP20 소켓
15	1	만능기판

Reference

Wikipedia: ‘Linear-feedback_shift_register’
New Wave Instruments: ‘Linear Feedback Shift Registers – Implementation, M-Sequence Properties, Feedback Tables’

Twitter Facebook LinkedIn

Pseudo-random Number Dice

SUKJOON OH